算法总结-回溯法

发表于   |   分类于   |     |   阅读次数

回溯法是一种通过暴力穷举的方式解决问题的方式，是深度优先搜索的一种具体应用。其思路不难理解，想象一下你在走一个迷宫，当在一个路口有A， B， C 三条岔路的时候你要怎么办呢？ 大家可以很容易地想到先尝试道路A， 如果走不通就回到这个路口尝试道路B，如果还走不通就尝试道路C，这就是一个典型地应用回溯法的例子。如果将目光着眼于整个迷宫，就可以发现这个迷宫其实就是一颗多叉树，每个路口就是一个节点，每个路口的岔路就是这个节点的子树，在这颗多叉树上应用深度优先搜索就是回溯法。LeetCode上关于回溯法的题目一般比较偏难，但是不管是如何变化，其解决的思路都是不变的，甚至有一定的“套路”可以解决大部分的问题。下面我们结合具体的题目来总结一下回溯法的使用。

LeetCode78

题目链接： https://leetcode.com/problems/subsets/

题目描述：
给定一个不包含重复数字的数组，返回所有的数组的子集并且不能有重复。

例子：

1
2
3
4
5
6
7
8
9
10
11
12
Input: nums = [1,2,3]
Output:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

题目分析：
如果不熟悉回溯法可能难以想到这道题可以用回溯法来解决，实际上这是一道很典型的回溯法题目，现在的关键是如何来构建这颗多叉树呢？首先我们创建一个数据为空的根节点，将数组中所有的数字都作为其子节点，对任何一个节点都将数组中这个节点数据后面所有的数看作子节点，这样上面的列子就可以构建成一棵如下所示的树。然后我们应用回溯法也即我们上文中总结过的深度优先遍历来遍历整棵树，并将所有的路径都记录下来就是最终要返回的结果。

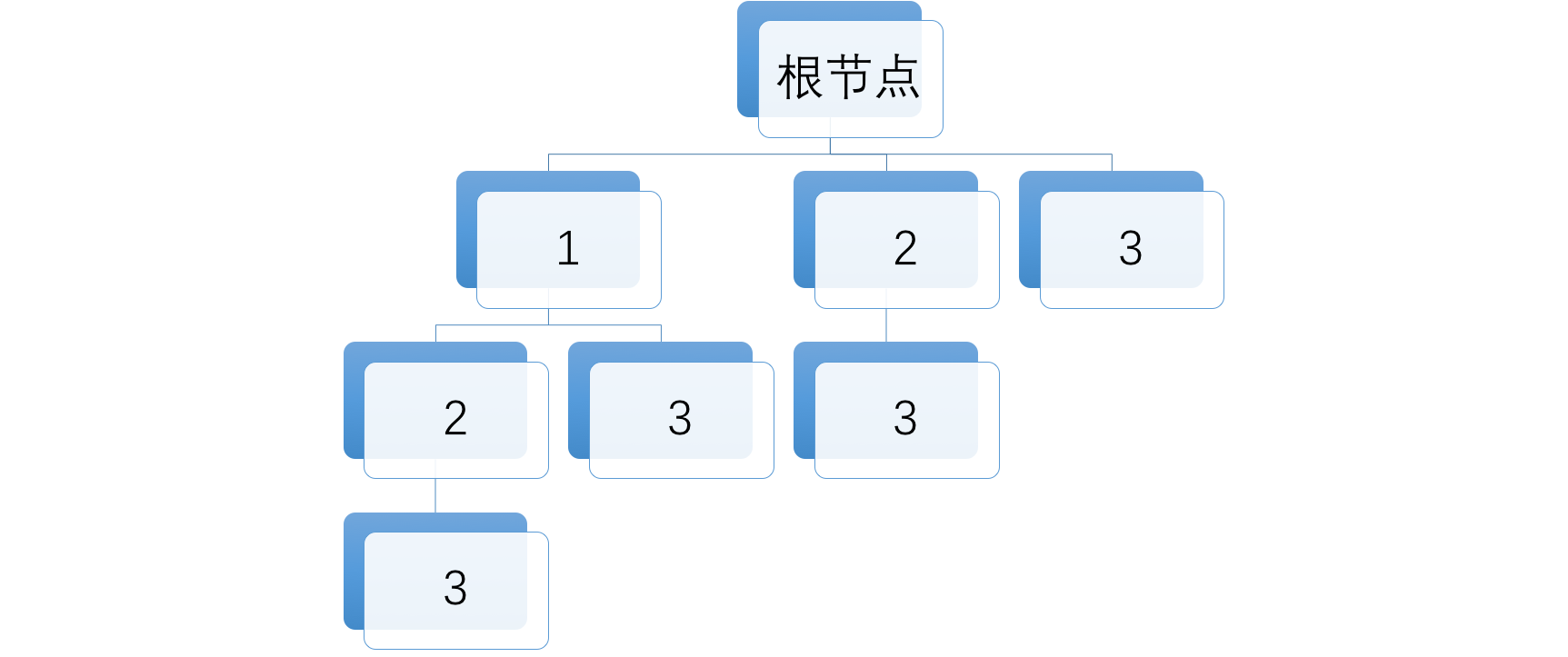
backtracking1.png

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
vector<vector<int>> subsets(vector<int>& nums) {
    vector<vector<int>> result;
    vector<int> path;
    backtrack(nums, result, path, 0);
    return result;
}
    
void backtrack(vector<int>& nums, vector<vector<int>>& result, vector<int>& path, int index){
    vector<int> temp = path;
    result.push_back(temp);
    for(int i = index; i< nums.size(); i++) {
        path.push_back(nums[i]);
        backtrack(nums, result, path, i + 1);
        path.pop_back();
    }
}

代码分析：

在代码中我们创建了一个二维数组result来保存所有的结果，使用数组path来记录当前的路径数据。当我们第一次调用调用backtrack方法的时候，path为空，代表了根节点，将其插入到result中，之后每次递归调用都将当前的路径最为一个结果插入到result中。接下来的的循环就是遍历当前节点的所有子节点，对每个子节点进行三步操作：

  1. 将子节点的数据插入到path中。
  2. 递归地对这个子节点进行深度遍历。
  3. 从path中移除当前的子节点，对下一个子节点进行同样的操作。

上述代码是回溯法的一个基本应用，也可以说是回溯法的一个“套路”，大部分回溯法的题目都是在这个”套路“的基础上做一些改变来实现的，让我们来看一下下个题目加深对回溯法的理解。

LeetCode90

题目链接： https://leetcode.com/problems/subsets-ii/

题目描述：
给定一个含有重复数字的数组，返回所有的数组的子集并且不能有重复。
例子：

1
2
3
4
5
6
7
8
9
10
Input: [1,2,2]
Output:
[
  [2],
  [1],
  [1,2,2],
  [2,2],
  [1,2],
  []
]

题目分析：
这道题是在上一题的基础上做了一点改变就是数组中含有重复的数字，我们在遍历的过程中要想办法来消除掉重复，那么如何才能做到呢？其实很简单，首先我们对整个数组进行排序，这样重复的数字就会靠在一起，然后我们在构建多叉树的时候对于重复的数字只用一次即可。如例子中有两个2，那么根节点下面的子节点就只有一个2。按照这种思路例子中的数组可以构建成如下所示的多叉树。

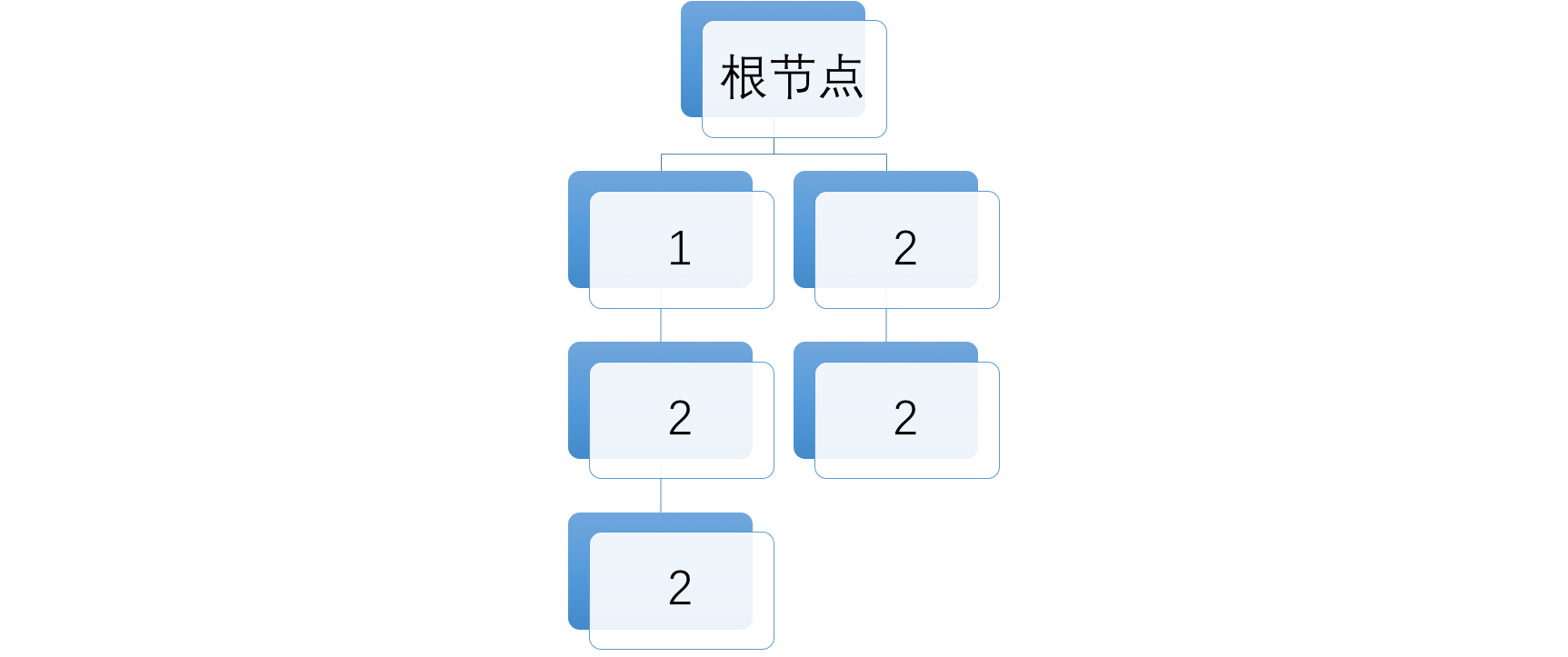
backtracking2.png

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
    vector<vector<int>> result;
    vector<int> path;
    sort(nums.begin(), nums.end());
    backtrack(nums, result, path, 0);
    return result;
}
    
void backtrack(vector<int>& nums, vector<vector<int>>& result, vector<int>& path, int index){
    vector<int> temp = path;
    result.push_back(temp);
    for(int i = index; i< nums.size(); i++) {
        if(i > index && nums[i] == nums[i - 1]) continue;
        path.push_back(nums[i]);
        backtrack(nums, result, path, i + 1);
        path.pop_back();
    }
}

代码分析：
在调用backtrack方法前，我们首先对数组进行了排序。在backtrack方法内的循环，我们判断当前的数字是否和上一个数字是重复的，如果是重复的则直接略过，这样就相当于将相同的数字在这一层给合并起来了。

LeetCode46

题目链接： https://leetcode.com/problems/permutations/

题目描述： 给定一个不包含重复的数组，返回所有可能的排列。

例子:

1
2
3
4
5
6
7
8
9
10
Input: [1,2,3]
Output:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

题目分析：

要应用回溯法来解决这道题关键是如何来构建这颗查找树？我们可以首先创建一个空的根节点，将数组中的所有的数字都作为其子节点，然后对每个节点，都将数组中其余的数作为这个节点的子节点。考虑到需要排除重复的数，在添加子节点的时候要排除当前节点到根节点路径上的所有的数。由于返回的数组长度都同远数组一致，所以加上空的根节点后整棵树的高度应该是 n + 1。例子中的数组可以构建成如下所示的树。树构建好之后，每个从根节点到叶子节点的路径就是一个可能的数组。

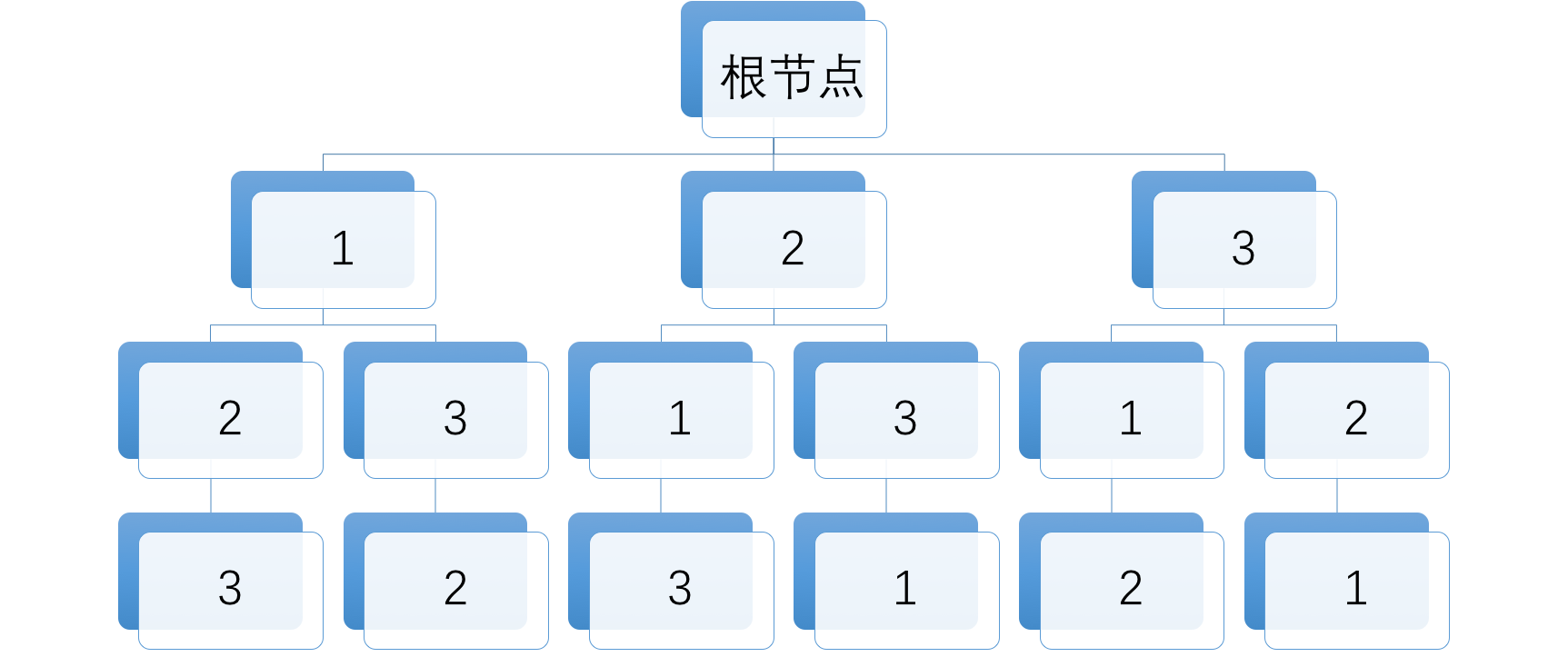
backtracking3.png

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
vector<vector<int>> permute(vector<int>& nums) {
    vector<vector<int>> result;
    vector<int> path;
    backtrack(nums, result, path);
    return result;
}
    
void backtrack(vector<int>& nums, vector<vector<int>>& result, vector<int>& path){
    if(path.size() == nums.size()){
        vector<int> temp = path;
        result.push_back(temp);
    }else{
        for(int i = 0; i< nums.size(); i++) {
            if(find(path.begin(), path.end(),nums[i]) != path.end()) continue;
            path.push_back(nums[i]);
            backtrack(nums, result, path);
            path.pop_back();
        }
    }
}

代码分析：
只有当path的长度和原数组长度一致的时候，说明我们找到了一种可能的结果将其记录下来；否则我们就需要循环整个数组来构建其子节点。在构建每个子节点前，我们在path中查找一下当前的数字是否已经包含在父节点之中了，已经包含过的数字需要排除掉。满足条件的数字会作为当前的节点插入到path中，并进行递归地遍历。

LeetCode51

题目链接： https://leetcode.com/problems/permutations/[](https://leetcode.com/problems/permutations/)

题目描述：
n皇后问题，将n替换成8就是经典的8皇后问题。在国际象棋中，皇后可以沿着竖排、横排、双向对角线进行攻击，题目要求给定一个整数n, 在一个n * n的棋盘上放置n个皇后，并且这些皇后彼此之间都攻击不到对方，返回所有可能的结果。如针对8皇后问题，下图就是一个解，每个皇后都攻击不到别的皇后。

例子

1
2
3
4
5
6
7
8
9
10
11
12
Input: 4
Output: [
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]

题目分析：
之前的题目都是遍历一个一维的数组，这个题目遍历的是一个二维数组，我们还是可以一样应用回溯法来解决。我们可以从第一行开始尝试每个位置，当我们在第一行中放置一个皇后后，当前行肯定不能再插入了，就需要在下一行中找到一个合法的位置放置下一个皇后。而为了判断某个位置是否能够放置皇后，我们还需要创建一个 n * n 大小的二维数组来记录已经放入皇后的位置。这样当我们放置了n个皇后后就找到了一个解。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
vector<vector<string>> solveNQueens(int n) {
    vector<vector<int>> tag(n, vector<int>(n));
    vector<vector<string>> result;
    find(result, tag, 0, n);
    return result;
}
    
void find(vector<vector<string>>& result, vector<vector<int>>& tag, int row, int n) {
    if(row == n){//找到一个解
        result.push_back(convert(tag, n));
        return;
    }
    
    for(int i = 0; i < n ;i++){
        if(isValid(result, tag, row, i, n)){
            tag[row][i] = 1;
            find(result, tag, row + 1, n);
            tag[row][i] = 0;
        }
    }
}
    
bool isValid(vector<vector<string>>& result, vector<vector<int>>& tag, int row, int column, int n) {
    for(int i = row - 1; i >= 0; i--){
        if(tag[i][column]) return false; //向上检查竖排
    }

    for(int i = row - 1, j = column - 1; i >=0 && j >=0; i--, j--){
        if(tag[i][j]) return false;//检查左上对角线
    }
    
    
    for(int i = row -1, j = column + 1; i >=0 && j < n; i--, j++){
        if(tag[i][j]) return false;//检查右上对角线
    }
    return true;
}
    
vector<string> convert(vector<vector<int>>& tag, int n){
    vector<string> solution;
    for(int i = 0; i < n; i++){
        string row = "";
        for(int j = 0; j < n; j++){
            row += tag[i][j]? "Q": ".";
        }
        solution.push_back(row);
    }
    return solution;
}

代码分析：
我们创建了二维数组tag来记录当前已经放置了皇后的位置， 然后从第一行开始遍历每一列， 如果当前的位置是合法的，就在tag中记录下这个位置，并递归地在下一行中进行深度遍历。 因为我们是一行行进行遍历的，所以当检查一个位置是否合法的时候只需要检查向上的竖排、左上对角线和右上对角线是否已经有皇后，下面还未遍历到是肯定没有放置皇后的。

当行数row等于n时，说明我们已经放置了n个皇后找到了一个解，这时候就可以根据tag中记录的皇后放置位置来生成一个解并插入到result中。

最后总结一下回溯法的”套路“：

  1. 根据需要将原始数组进行排序。
  2. 创建递归方法，将记录结果的result,记录路径的path, 记录坐标的index等作为参数。
  3. 在递归方法内部根据条件决定是否将当前的path等插入到result中。
  4. 深度优先遍历所有满足条件的子节点，记录当前状态，调用递归方法进入下一层，最后恢复状态。

虽然回溯法的题目在LeetCode中以中等和困难级别居多，但是如果掌握了上述的套路，相信绝大部分的题目都将不是问题。

signature.png