算法总结-二分查找法

在LeetCode的题目讨论中，经常会有些大神将某一类的题目结题思路给整理了出来，感觉受益匪浅。受之启发，萌生了自己也总结一下常见算法的解题思路的想法，希望可以让自己在这个总结的过程中可也融汇贯通这些思路，同时可以给后来者以启发。

从哪里开始好呢？就从经典的二分查找法开始吧，这个算法几乎所有学过计算机的人都知道，而且我在之前的面试中不止一次碰到过这个算法以及这个算法的变种。
二分查找法的思路就是通过条件判断每次淘汰掉一半的数据，从而可以达到一个非常快的查找速度。下面我们结合具体的题目来看一下。

LeetCode35

题目链接： https://leetcode.com/problems/search-insert-position/

题目描述： 在一个递增的有序不重复的数列中查找一个目标数字，如果找到就返回这个数字的index, 否则返回这个数字应该插入到数列中的index。

思路: 这是一道最基础的二分查找题，每次拿出序列中间的数并和目标数字进行比较，会有三种情况：

1. 这个数恰好等于目标数字，找到了，返回index。
2. 这个数比目标小说明目标在右半边的序列中，淘汰掉左半边。
3. 这个数比目标大说明目标在左半边的序列中，淘汰掉右半边。
   当出现2、3这两种情况时，我们就在对应的半边序列中递归地重复上述判断,直到这半边的序列为空位止，这时就说明序列中并没有对应的数字，直接返回当前的index。

代码： 有递归和非递归两种实现，这里使用非递归的方式。代码由C++来实现。

int searchInsert(vector<int>& nums, int target) {
    int l =0;
    int r = nums.size() - 1;
    while(l <= r) {
        int mid = l + (r - l) / 2;
        if(nums[mid] == target) {
            return mid;
        }else if(nums[mid] > target){
            r = mid -1;
        }else{
            l = mid + 1;
        }
    }
    return l;
}

代码分析： 由于每次判断都能去掉一半的数字所以时间复杂度是O(logN)。还有几个细节需要注意下：

1. 为什么 while 循环的条件是 l <= r 而不是 l < r 呢？对于这种边界的判断我们只要考虑一下极端情况下回如何就好，如在只有一个数字 0 的数列中查找 0，这种情况下 l 和 r 都是 0， 如果使用 l < r 作为判断条件很明显是不会进入 while 循环进行判断的。
2. 为什么不用int mid = (l + r) / 2的方式求 mid 的值呢？ 当数列的长度很大的时候，l + r 有可能超出 int 的最大值导致溢出，所以代码中的方式较为健壮。
3. 为什么不相等后 r 和 l 的值不是赋值成 mid，而是要 -1 和 +1 呢？如果不相等，说明无轮如何 nums[mid] 都不应该被包含进下一轮的判断，通过 -1 和 +1 来将其砍掉。

LeetCode34

题目链接： https://leetcode.com/problems/find-first-and-last-position-of-element-in-sorted-array/
题目描述：
这是一道二分查找法的变种。需要在一个含有重复数字的递增数列中找到目标数字的起始和结束的 index，没有的话返回{-1, -1}。

思路： 很多人看到这个题目后的最初想法估计都是直接从前面和后面按顺序查找，但是直接查找的复杂度是 O(N)，并不是一个好的方案。我们还是要从二分查找法入手，但是换一种思路，使用二分法实现一个方法找到一个数在数列中最左侧的 index, 没有的话就返回其插入位置，这样起始位置可以直接用这个方法，结束的位置可以通过查找目标数 +1 的方式来实现。

所以问题就成了如何找到重复数字最左侧的 index, 同上面一样，我们还是取中间位置的数同目标数字进行对比，此时却只有两种状态了：

1. 中间数比目标数字小，说明目标数字在右半序列中，淘汰掉当前位置和左半边。
2. 中间数大于或者等于目标数字，这里再分三种情况：
   1. 中间数大于目标数字，结果在左半边序列中，淘汰掉当前位置和右半边。
   2. 中间数等于目标数字，但是不是最左侧的，结果在左半边序列中，淘汰掉当前位置和右半边。
   3. 中间数等于目标数字，而且就是最左侧的，此时如果也淘汰掉当前位置和右半边的话，左侧的 l 坐标在退出循环的时候就会指向当前的这个位置，恰好是返回值。

代码：

vector<int> searchRange(vector<int>& nums, int target) {
    int left = findLeftIndex(nums, target);
    //在序列中没有target, 直接返回。
    if(left == nums.size() || nums[left] != target) return {-1 , -1};
    int right = findLeftIndex(nums, target + 1) - 1;
    return {left, right};
}

//返回target最左侧的index, 如果没有则返回target应该插入的index。
int findLeftIndex(vector<int>& nums, int target){
    int l = 0;
    int r = nums.size() - 1;
    while(l <= r){
        int mid = l + (r - l) / 2;
        if(nums[mid] < target){
            l = mid + 1;
        }else{
            r = mid - 1;
        }
    }
    return l;
}

代码分析： 当我们查找到 target 的起始位置后，需要判断序列中是否含有 target, 没有的话就可以直接返回了，否则可以继续找结束位置。在这里我们查找 target + 1 的最左侧的index, 这样，无论数列中是否含有 target + 1, 这个index - 1 都是 target 在数列中的结束位置。

LeetCode74

题目链接： https://leetcode.com/problems/search-a-2d-matrix/
题目描述：
有一个二维数组，每一行中的数字都是递增的，而且比上一行的数字都要大，查找一个数是否在这个数组中。

思路： 这个二维数组其实就是一个递增的一维数组将其给拆成多个子数列，所以我们可以直接使用二分法进行查找，只要处理好序列的坐标即可。

代码：

 bool searchMatrix(vector<vector<int>>& matrix, int target) {
    if (!matrix.size() || !matrix[0].size()) return false;
    int m = matrix.size();
    int n = matrix[0].size();
    int i = 0; 
    int j = m * n - 1;
    while(i <= j){
        int mid = i + (j - i) / 2;
        if(matrix[mid / n][mid % n] == target) return true;
        else if(matrix[mid / n][mid % n] > target) j = mid -1;
        else i = mid + 1;
    }
    
    return false;
}

代码分析： 这个 m 行 n 列的二维数组总共有 m * n 个数字，我们直接将其看成一个一维数组来计算 mid，然后通过 mid / n 得到行坐标， 通过 mid % n 得到列坐标，这样就可以确定这个中间的数。

LeetCode240

题目链接： https://leetcode.com/problems/search-a-2d-matrix-ii/
题目描述：
有个 m 行 n 列的二维数组，每一行从左到右递增，每一列是从上到下递增，在这个二维数组里查找是否存在一个数。

思路: 这道题不使用二分法的话思路会比较明确些。我们可以从二维数组的右上角做为起点，取这个位置的数同目标数字进行对比，同样会有三种情况：

1. 相等。找到了这个数，直接返回true。
2. 比目标数字大，说明结果应该在当前位置的左侧，所以将列坐标 -1。
3. 比目标数字小，说明结果应该在当前位置的下方，将行坐标 +1。

重复整个过程直到找到或者坐标越界为止。

代码：

bool searchMatrix(vector<vector<int>>& matrix, int target) {
    if(matrix.size() == 0 || matrix[0].size() == 0) return false;
    int row = matrix.size();
    int col = matrix[0].size();
    int i = 0;
    int j = col - 1;
    while(i < row && j >= 0){
        if(matrix[i][j] == target) return true;
        else if(matrix[i][j] < target) i++;
        else j --;
    }
    return false;
}

代码分析： 查找的过程其实就是一条折线，时间复杂度为O(m + n)，

二分法思路：
这个二维数组的特点就是左上角数字最小，右下角数字最大，整体从左上角向右下角递增。如果我们使用二分查找法确定其中心点，就可以将这个二维数组分解成4个小的二维数组，如下图所示，我们分别用1， 2，3，4 来代表。而且这4个小的二维数组都满足左上角数字最小，右下角数字最大，，整体从左上角向右下角递增的特点。看到这里我们应该想到可以使用递归来解决这个问题。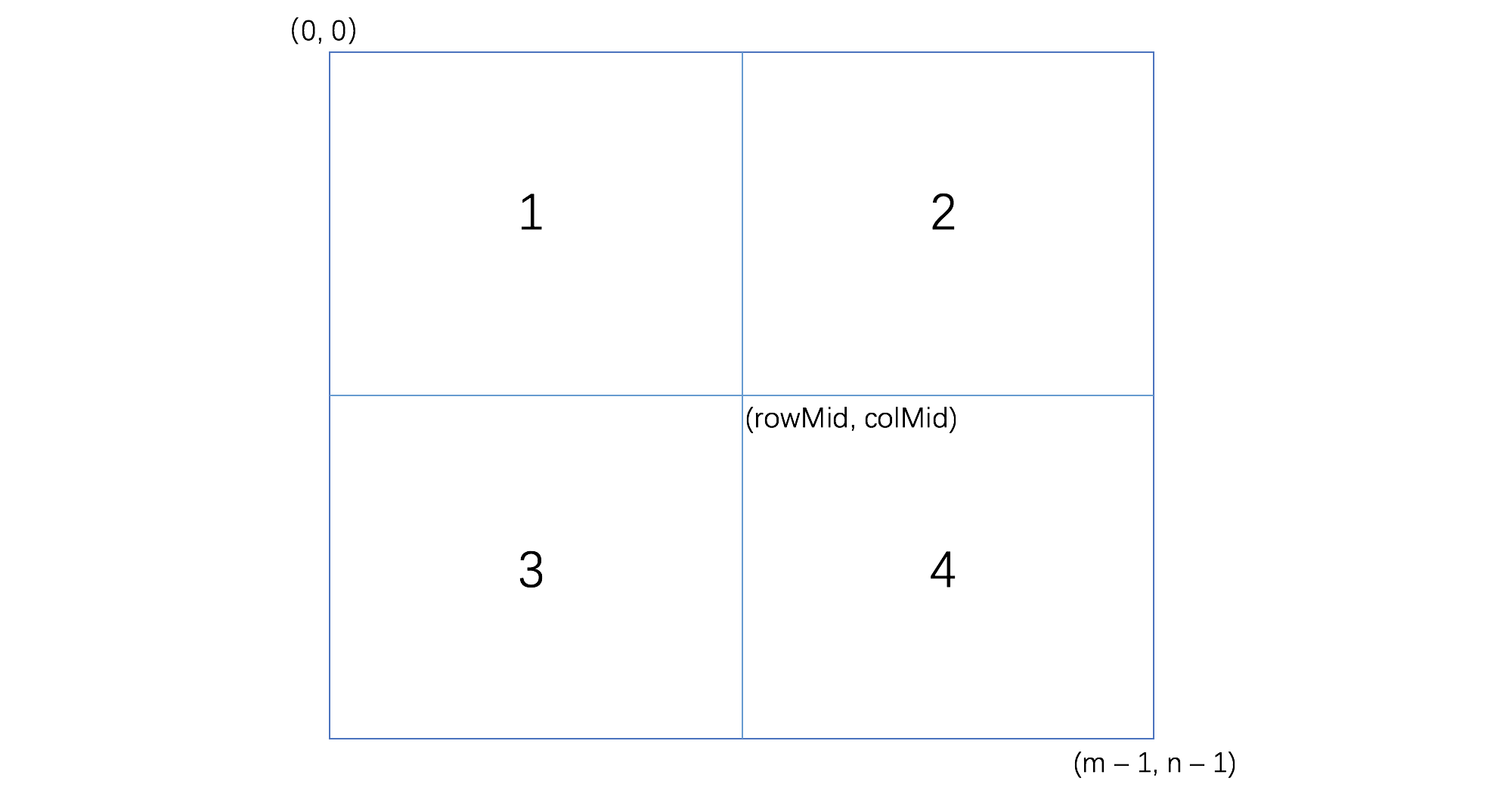

确定中心点后，我们将中心位置的数据 center 和目标 target 进行比较分析，然后分别讨论下面三种情况：

1. center == target, 直接返回 true。
2. center > target, center是数组4中的最小数字，所以数组4就可以淘汰掉。
3. center < target, center是数组1 中的最小数字，所以数组1可以淘汰掉。

递归地在剩下的3个小数组中寻找target。

代码：

bool searchMatrix(vector<vector<int>>& matrix, int target) {
    if(!matrix.size() || !matrix[0].size()) return false;
    return find(matrix, 0, matrix.size() - 1, 0, matrix[0].size() - 1, target);
}

bool find(vector<vector<int>>& matrix, int rowStart, int rowEnd, int colStart, int colEnd, int target){
    if(rowStart > rowEnd || colStart > colEnd) return false;
    int rowMid = (rowStart + rowEnd) / 2;
    int colMid = (colStart + colEnd) / 2;
    if(matrix[rowMid][colMid] == target) return true;
    else if(matrix[rowMid][colMid] > target){
        //合并的数组1和3
        return find(matrix, rowStart, rowEnd, colStart, colMid -1, target) ||
        //数组2
            find(matrix, rowStart, rowMid - 1, colMid, colEnd, target);
    } else {
        //合并的数组2和4
        return find(matrix, rowStart, rowEnd, colMid + 1, colEnd, target) ||
        //数组3
            find(matrix, rowMid + 1, rowEnd, colStart, colEnd, target);
    }
}

代码分析：
每次判断可以淘汰掉 1 / 4 的数据，然后重新在剩下的3个小数组中进行递归地搜索，代码中使用了一个优化技巧，就是在淘汰数组4的时候将数组1和3合并成一个数组进行递归，淘汰数组1的时候合并数组2和4。这个算法的时间复杂度为log((4/3), m *n)，在LeetCode中测试发现其效率反而不如上面那个效率高。