算法总结-深度优先算法

发表于   |   分类于   |     |   阅读次数

深度优先算法多数是应用在树上，一个比较典型的应用就是二叉树的中序遍历。所谓树的前、中、后序遍历都是以树的根节点为准的，如下图所示的二叉树中序遍历的结果就是 4，2，5，1，6，3，7。下面我们来看一下 LeetCode 中的二叉树中序遍历的题目。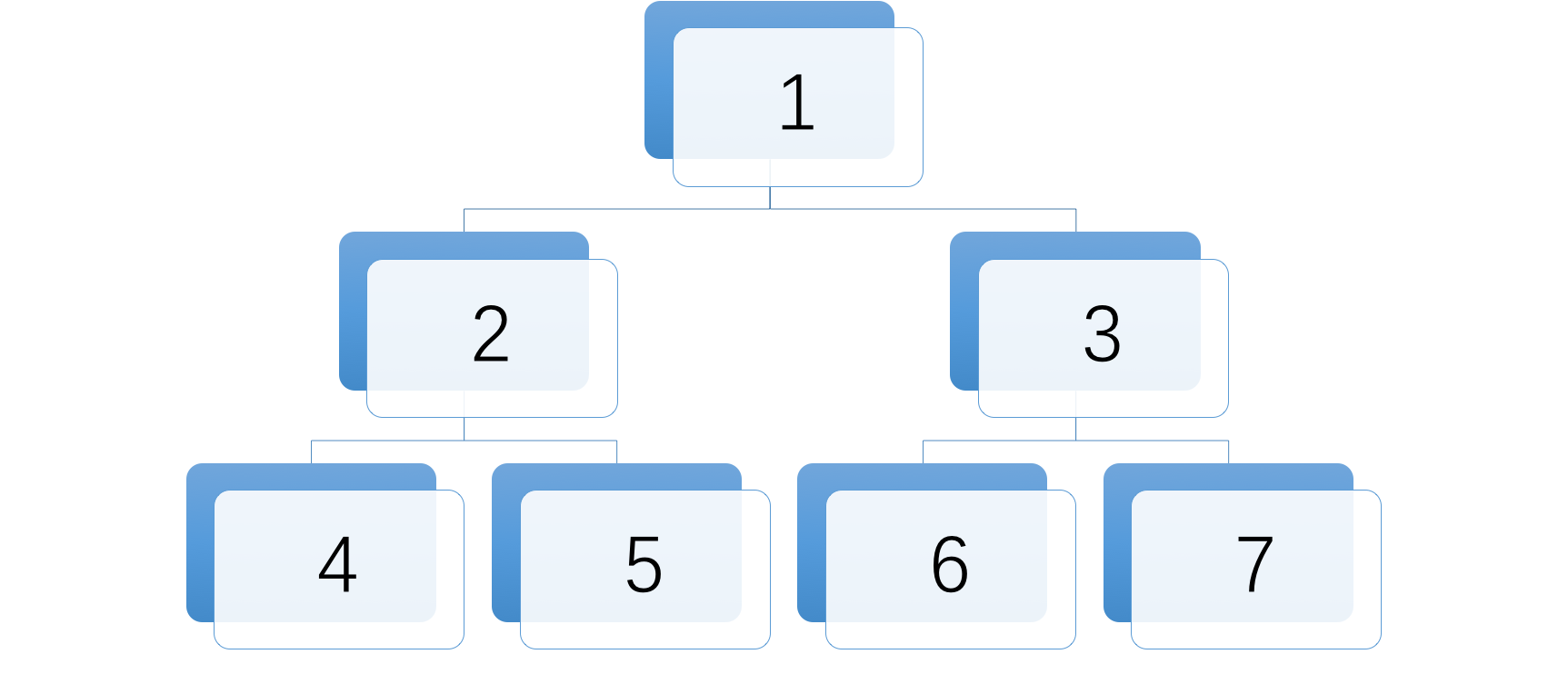
dfs_parenttheses1.png

LeetCode94

题目链接： https://leetcode.com/problems/binary-tree-inorder-traversal/

题目分析： 树的遍历都有递归和非递归两种方式，对中序非递归来说需要使用栈的帮助来实现，我们需要从根节点出发寻找当前树的最左下角的叶子节点，并将路径上的节点都进栈。当找到后，再根据栈中存储的节点来依次遍历其根节点和右子树。

非递归代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
vector<int> inorderTraversal(TreeNode* root) {
    vector<int> nodes;
    stack<TreeNode*> path;
    while (root || !path.empty()) {
        while (root) { //寻找当前节点的最左下的叶子节点
            path.push(root);
            root = root -> left;
        }
        root = path.top();
        path.pop();
        nodes.push_back(root -> val);//遍历当前节点
        root = root -> right;//继续遍历右子树
    }
    return nodes;
}

代码分析：
代码主体是由两个 while 循环构成的，外层的循环确保了可以遍历到整棵二叉树，而内层循环则是寻找到当前节点下的最左下的叶子节点。每个节点都会进栈、出栈一次，所以时间复杂度为O(N)。

中序遍历的递归算法非常简洁明了，无需多说，可以直接看代码。

递归代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> nodes;
        inorder(root, nodes);
        return nodes;
    }
private:
    void inorder(TreeNode* root, vector<int>& nodes) {
        if (!root) {
            return;
        }
        inorder(root -> left, nodes);
        nodes.push_back(root -> val);
        inorder(root -> right, nodes);
    }
};

代码分析：
inorder方法中的参数我们使用了&符号来确保了nodes传入的是引用，这样就会确保整个遍历过程只有一个我们在外面定义的vector<int> nodes。内部递归地调用顺序就是遍历的顺序，所以如果我们将nodes.push_back(root -> val)同上面的递归调用交换，就变成了前序遍历，同理同下面的递归调换就变成了后序遍历。每个节点都会被访问一次，所以递归算法的时间复杂度同样是O(N)。

LeetCode230

题目链接： https://leetcode.com/problems/kth-smallest-element-in-a-bst/

题目描述：
在一棵二叉查找树中选择第 k 小的数，所谓二叉查找树就是树中每个节点都满足以下条件：左子树中所有的节点都小于根节点，而右子树中所有的节点都大于根节点。

题目分析：
对于二叉查找树来说，其中序遍历结果就是一个递增的数列，所以在中序遍历的过程中遍历到的第 k 个数也就是我们要找得第 k 小的数。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
public int kthSmallest(TreeNode root, int k) {
	Stack<TreeNode> stack = new Stack<>();
	while(root != null || !stack.isEmpty()) {
	 while(root != null) {
	     stack.push(root);    
	     root = root.left;   
	 } 
	 root = stack.pop();
	 if(--k == 0) break;
	 root = root.right;
	}
	return root.val;
}

代码分析：

这里我们使用非递归的方式，每次出栈操作意味着遍历一个节点， 所以将 k - 1，而 k 被减到 0 的时候就是遍历到了第 k 个数，可以直接退出循环并返回结果。

LeetCode98

题目链接： https://leetcode.com/problems/validate-binary-search-tree/

题目描述：
给定一颗二叉树，判断是否是一棵二叉查找树。

题目分析：
在上一题中我们已经知道了对二叉查找树进行中序遍历的结果是个递增的数列，所以要判断一棵二叉树是否是二叉查找树只需要对其进行遍历，然后判断其结果是否是递增的即可

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public boolean isValidBST(TreeNode root) {
   if (root == null) return true;
   Stack<TreeNode> stack = new Stack<>();
   TreeNode pre = null;
   while (root != null || !stack.isEmpty()) {
      while (root != null) {
         stack.push(root);
         root = root.left;
      }
      root = stack.pop();
      if(pre != null && root.val <= pre.val) return false;
      pre = root;
      root = root.right;
   }
   return true;
}

代码分析：
在进行中序遍历的过程中，我们使用一个名为pre的对象记录下前一个节点，然后在遍历的过程中如果出现前面的节点值大于当前的节点的时候，我们就可以认为这棵树不是一颗二叉查找树，从而直接返回false，而无需去遍历后面的节点了。

LeetCode301

题目链接： https://leetcode.com/problems/remove-invalid-parentheses

题目描述： 在一个字符串中含有一些(和)，需要删除最少的括号让这个字符串成为一个合乎规则的字符串，即每个(都有一个与之对应的)。返回所有的可能结果。

例子1：

1
2
Input: "()())()"
Output: ["()()()", "(())()"]

例子2：

1
2
Input: "(a)())()"
Output: ["(a)()()", "(a())()"]

例子3：

1
2
Input: ")("
Output: [""]

题目分析：
这是一道困难级别的题目，比较有挑战性，可以用深度优先的思路来解决。我们分情况来分析一下，看看如何来决定字符的取舍：

  1. 对于非括号的字符，肯定是都需要保留的。
  2. 对于每个(， 我们都可以尝试着保留或者去掉。
  3. 对于每个)， 同样我们可以尝试着保留或者去掉。

基于上面的分析，如果将字符串里的每个字符作为一层的话，那我们就可以根据上面的3条结论来创建一棵树，如可以将字符串"a()"构建成一棵如下所示的树。很明显最后正确的返回应该是保留所有的字符串，也就是从根节点一直沿着左子树到叶子节点的路径。

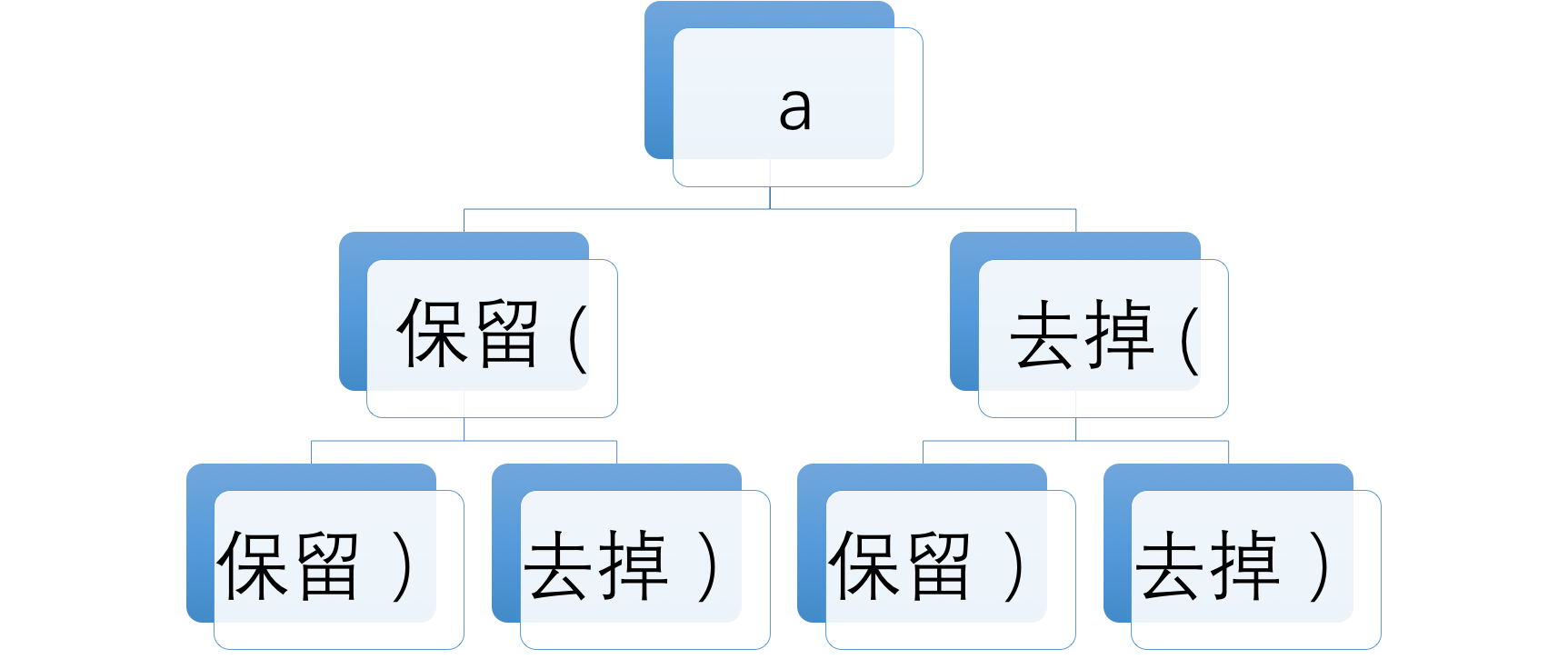
dfs_parenttheses.png

这么一看似乎也不是很难嘛，怎么对得起困难的级别呢？别急，让我们在看另外一个要求：需要删除最少的括号。那么如何来确定需要删除的最少括号数量呢？我们再来具体分析一下哪些括号是不合乎规则的：

  1. 对于)，我们需要确定前面有多少个还未配对的(，如果当前)的数目已经超过了还未配对的(的数目，那么这就是需要删除的。
  2. 对于(， 我们需要确定后面有多少个)，超出)数目的(也都是要删除的。

如例子3中第一个)， 在它之前并没有未配对的(，所以它是需要删除的。对于后面的(，在其之后也没有能与之配对的)，所以这个括号也是需要删除的。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
vector<string> removeInvalidParentheses(string s) {
    int left = 0, right = 0;
    unordered_set<string> result;
    
    for(auto c : s){
        if(c == '(') left++;
        else if(c == ')') {
            if(left > 0) left--;
            else right++;
        }
    }
    
    dfs(0, 0, left, right, s, "", result);
    return vector<string>(result.begin(), result.end());
}

void dfs(int pair, int index, int left, int right, const string& s, string solution, unordered_set<string>& result){
    if(index == s.size()){
        if(pair == 0 && left == 0 && right == 0) result.insert(solution);
        return;
    }
    if(s[index] == '('){
        if(left > 0)  dfs(pair, index + 1, left - 1, right, s, solution, result);
        dfs(pair + 1, index + 1, left, right, s, solution + s[index], result);
    }
    else if(s[index] == ')'){
        if(right > 0) dfs(pair, index + 1, left, right - 1, s, solution, result);
        if(pair > 0) dfs(pair - 1, index + 1, left, right, s, solution + s[index], result);
    }
    else{
        dfs(pair, index + 1, left, right, s, solution + s[index], result);
    }
}

代码分析：

我们首先遍历一遍整个字符串，并统计一下字符串中需要删除的两种括号的数量，然后使用dfs方法来进行深度优先遍历所有可能的结果。参数left和right分别代表了目前需要删除的左右括号数目；solution记录了当前的临时结果，也就是从根节点到当前节点路径上所有的字符组合；pair代表了目前左右括号数目是否是配对的，只有遍历到最后一个字符并且pair，left和right都为0时，说明我们找到了一个合法的结果，为了去掉重复的结果，我们使用了set来暂时保存结果，并在遍历结束后将其转换成一个vector返回。
当我们遍历到一个(字符时，如果left > 0说明还有需要删除的(， 所以我们可以删除这个括号同时将index + 1进入一层的遍历；无聊是否还有需要删除的(， 我们都要尝试保留这个括号并进入下一层的遍历。对于)， 应用同样的逻辑。而对于非括号的字符，肯定是需要保留的，所以直接进入下层遍历。

最后来看一下时间复杂度，在原字符串合法的情况下left和right都是0，每次递归也只有一个分支，所以复杂度为O(N)；最坏的情况下，字符串中只包含非法的括号，如上面的例子3，所以每次递归都会有两个分支，时间复杂应该为O(N2)。

深度优先算法是回溯法的基础，回溯法可以用来解决很多问题如著名的八皇后问题等。在下篇文章中，我们来一起探讨一下回溯法的使用。

signature.png