算法总结-归并排序

发表于   |   分类于   |     |   阅读次数

归并排序是分治法的一种应用，其思路是将数组分为左右两部分，分别递归地进行归并排序，然后将这两部分给合并起来。归并排序的c++递归实现可以参考下面的模板：

1
2
3
4
5
6
7
 int mergeSort(iterator l, iterator r) {
    if (r - l <= 1) return; 
    iterator m = l + (r - l) / 2;
    int count = mergeSort(l, m) + mergeSort(m, r);
    inplace_merge(l, m, r);
    return count;
}

在上述代码中，l和r分别代表了需要排序的起始点和终点，需要注意的是这个区间是左闭右开的，也就是说l所指向的元素会参与到这轮排序中，而r不会。代码里用到的inplace_merge是c++的内置函数，会将左右两部分在数组内部给合并起来。

归并排序不仅可以用来排序。在上述代码中，当进行完左右两部分的递归排序，在调用inplace_merge进行合并之前，这个数组会有如下的特性：

  1. 左右部分都分别是有序递增的。
  2. 左半部分元素的index肯定是小于右半部分的。

结合上述的特性，我们只要在调用inplace_merge前做一些有针对性的处理就可以解决那些有两个index i, j， 当 i < j 时 nums[i] 和 nums[j] 满足某种条件的问题。

让我们结合具体的题目来看一下。

LeetCode315

题目链接：
https://leetcode.com/problems/count-of-smaller-numbers-after-self/

题目描述：
给定一个数组，要对数组中的每个数都计算出后面有多个比这个数小的数。
例子

1
2
3
4
5
6
7
Input: [5,2,6,1]
Output: [2,1,1,0] 
Explanation:
5的后面有2和1这两个比它小的数。
2后面有1这一个比它小的数。
6后面有1这一个比它小的数。
1后面没有比它小的数。

题目分析：
这道题目最简单的方式就是使用两重循环，对每个数都遍历一遍后面有多少个小于它的数。这种方法的时间复杂度是O(N2)，不是很理想，如果面试时只给出这种解法的话肯定是不会给通过的。所以我们要使用归并排序的方法来进行优化。

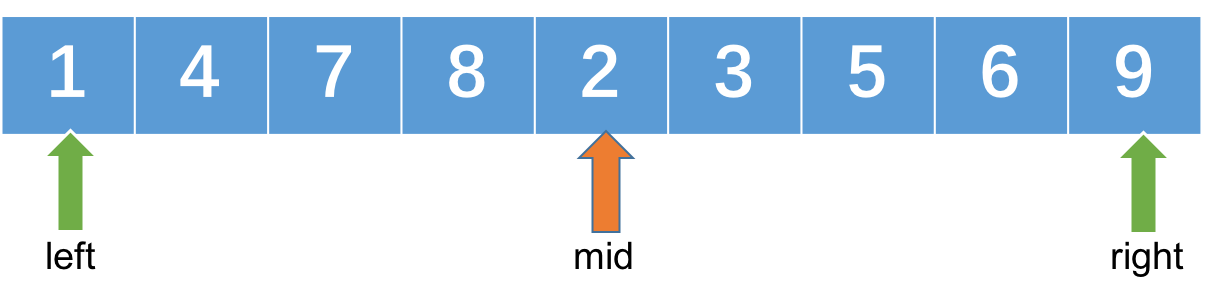
我们来思考一下，在归并排序进行合并操作前左右两部分都是排好序状态，因为题目要求的是计算后面有多少小于自己的数，所以对于左半部分的每个数都可以在右半部分中容易计算出满足条件的数；而对于右半部分的可以先忽略，在下一层的递归中进行处理。如下图所示，对于数字4，我们可以从mid开始往后遍历右半部分找到2、3这两个小于4的数，其他的数也都一样。这只是一层递归，当对左右两部分分别进行递归的时候需要进行相同的操作，而且要将所有的的结果都累加起来。

mergesort1.png

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#define iterator vector<pair<int,int>>::iterator
class Solution {
public:
    vector<int> countSmaller(vector<int>& nums) {
        int n = nums.size();
        if(n == 0) return {};
        vector<int> count(n);
        vector<pair<int,int>> pairs;
        for(int i = 0; i < n; i++){
            pairs.push_back({nums[i], i});
        }
        
        merge(pairs.begin(), pairs.end(), count);
        return count;
    }
    
    void merge(iterator left, iterator right, vector<int>& count){
        if(right - left <= 1) return;
        auto m = left + (right - left) / 2;
        merge(left, m, count);
        merge(m, right, count);
        auto j = m;
        for(auto i = left; i < m; i++){
            while(j < right && (*i).first > (*j).first) j++;
            count[(*i).second] += j - m;
        }
        inplace_merge(left, m, right);
    }
};

代码分析：
我们首先定义了count这个vector，并使用传引用的方式传入到递归方法中来记录递归过程中所有的结果。因为排序会改变原始的数据的位置，所以我们创建另外一个vector pairs来记录下每个数的位置。

在递归函数中，当right - left <= 1时说明现在要排序的数小于2个，无需进行排序可以直接返回。然后根据左右的坐标计算出中间坐标并对左右两边进行递归的排序操作。之后对左半部分的每个数都在右半部分中找出满足条件数的数量并保存到count中。最后使用c++的内置函数inplace_merge将左右两部分给合并起来。

归并排序的时间复杂度为O(NLog(N)), 这里做的改变就是在递归函数内添加了一个for循环，增加的时间复杂度为O(N)级别，所以总体的时间复杂度还是O(NLog(N))。

LeetCode327

题目链接：
https://leetcode.com/problems/count-of-range-sum/

题目描述：
给定一个数组和一个范围[lower, upper], 对这个数组进行分组求和，计算出这些分组和处于这个范围内的数量。

例子

1
2
3
4
5
6
7
8
9
Input: nums = [-2,5,-1], lower = -2, upper = 2,
Output: 3 
解释：
[0,0]的和为-2，处于范围内，数目+1。
[0,1]的和为3，超出范围。
[0,2]的和为2，处于范围内，数目+1。
[1,1]的和为5，超出范围。
[1,2]的和为4，超出范围。
[2,2]的和为-1，处于范围内，数目+1.

题目分析：
要使用归并排序的方法来解这道题需要首先将题目做一下转换。我们可以创建一个大小为 n + 1 的数组 sum，用 sum[i]代表前i项的和，这样就可以将题目转换成寻找 i 和 j, 使lower <= sums[j] - sums[i] <= upper。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    int countRangeSum(vector<int>& nums, int lower, int upper) {
        vector<long> sum(nums.size() + 1);
        for(int i = 0; i< nums.size();i++){
            sum[i+1] = sum[i] + nums[i];
        }
        
        int n =  merge(sum, 0, sum.size(), lower, upper);
        return n;
    }
    
    int merge(vector<long>& sum, int left, int right,int lower, int upper){
        if(right - left <= 1) return 0;
        int mid = left + (right - left) / 2;
        
        int count = merge(sum, left ,mid, lower, upper)
            + merge(sum, mid, right, lower, upper);
        
        for(int m = left, i = mid, j = mid; m < mid; m++){
            while(i < right && sum[i] - sum[m] < lower) i++;
            while(j < right && sum[j] - sum[m] <= upper) j++;
            count += j - i ;
        }
        
        inplace_merge(sum.begin() + left, sum.begin() + mid, sum.begin() + right);
        return count;
    }
};

代码分析：

首先创建 大小为 n + 1 的数组 sum，然后遍历数组并将前面所有数字累加的和填充到这个数组中。递归方法merge的返回值为left到right的范围内满足条件的组合数目。

在递归方法内，通过对左右两部分子集进行递归调用获取到这两部分中满足条件的组合数目，然后通过一个for循环统计那些横跨了左右两部分的满足条件的组合数目。特别注意到因为在左右两部分子集已经进行了递归的归并排序，这两个子集内的数据都是有序递增的，所以我们可以通过两个while循环找到以m开始的所有满足条件的集合数目。如下图所示的数组当lower = 1， upper = 2，m指向4的时候i和j最终的位置就会分别指向5和9，此时横跨左右两部分的组合数就为2。

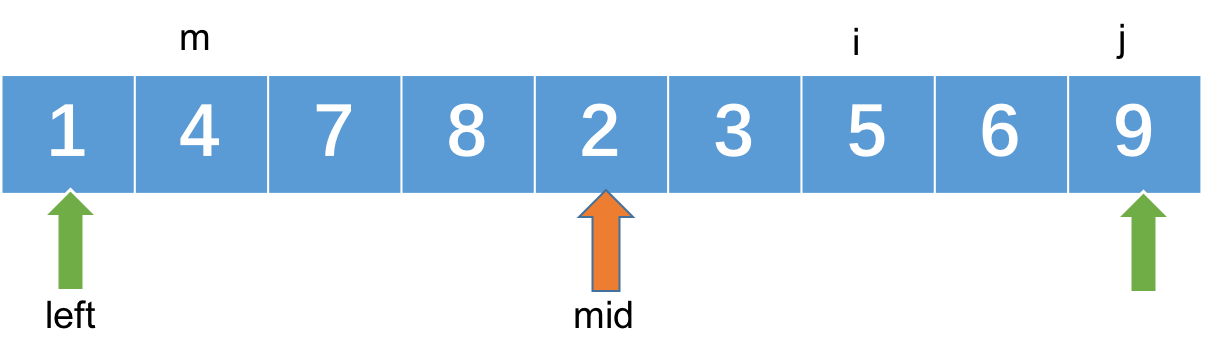
mergesort2.png

最后使用inplace_merge方法将左右两部分进行合并并将这些所有的结果加起来即为当前范围内所有满足条件的组合数目。

LeetCode493

题目链接：
https://leetcode.com/problems/reverse-pairs/

题目描述：
给定一个数组nums，如果两个数的index (i, j) 满足条件 i < j 并且 nums[i] > 2*nums[j]，那么这两个数就是一个重要交换对，需要返回数组中这样的重要交换对的数目。

例子:

1
2
3
4
5
Input: [1,3,2,3,1]
Output: 2

Input: [2,4,3,5,1]
Output: 3

题目分析： 这个题目可以很容易地通过归并排序来解决，只要在排序过程中判断一下左右两部分有多少对满足条件的数即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int reversePairs(vector<int>& nums) {
    return mergeSort(nums, 0, nums.size());
}
    
int mergeSort(vector<int>& nums, int left, int right){
    if(right - left <= 1) return 0;
    int mid = (left + right) / 2;
    int count = mergeSort(nums, left, mid)
        + mergeSort(nums, mid, right);
    
    for(int i = left, j = mid; i< mid; i++){
        while(j < right && nums[i] > nums[j] && nums[i] > 2l * nums[j]) {
            j++;
        }
        count += j - mid;
    }
    inplace_merge(nums.begin() + left, nums.begin() + mid, nums.begin() + right);
    return count;
}

代码分析：
在左右两部分排序结束后，遍历所有左半部分的数据在右半部分中查找满足条件nums[i] > 2*nums[j]的数据就是题目要求的重要交换对。特别注意这里使用2l * nums[j], 当nums[j]的数较大的时候，乘以2容易造成int类型的数据溢出，使用long类型可以防止此类错误。

上面三个题目都是困难级别的，如果不使用归并排序的话基本上只能采用两重循环这种效率低下的方法来解决。只要题目是查找数组中的两个坐标并要求坐标上对应的数组满足某种关系，我们都可以套用归并排序的模板来解决。需要牢记的是左右两部分排序后都是有序递增的，利用好这个特性可以帮助我们提高查找满足条件数据的效率。掌握上述模板后，相对来讲归并排序不是很难。

signature.png