算法总结-股票买卖

股票的买卖问题就是在已知股价波动情况和其它一些限制条件的前提下，合理地安排买卖的时间点来获取最高的利润，基本上都是通过贪心算法和动态规划来解决。下面结合具体的题目进行分析。

LeetCode121 股票买卖时机问题1

题目链接：
https://leetcode.com/problems/best-time-to-buy-and-sell-stock/

题目描述：

给定一个数组代表每天的股价，在只允许买卖一次的情况下找出可以得到的最高利润。

例子

Input: [7,1,5,3,6,4]
Output: 5
Explanation: 在第二天以价格1买得股票，然后再第5天以价格6卖出股票就可以得到最高的利润5

题目分析：
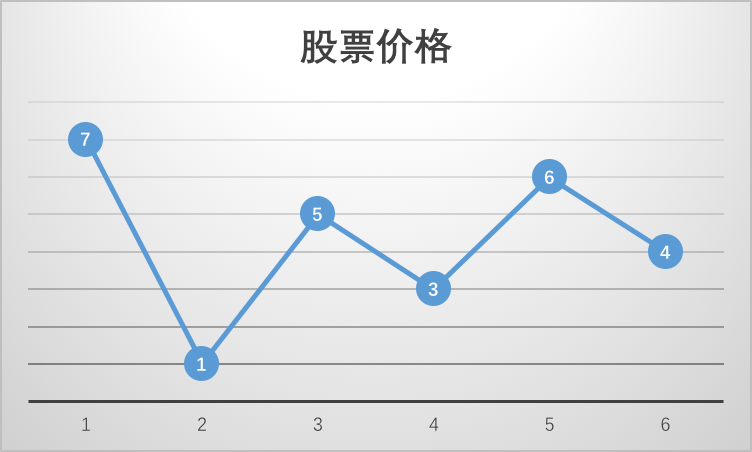
利润就是卖出的价格减去买入价格，想得到利润就需要在低价买入，然后在高价卖出，否则就是赔钱, 而想要获得最高的利润就需要让这个价格差最大。例子中股票价格可以绘制成如下所示的折线图，当在第二天以价格1买入后，后面的任何一天卖出都是获利的，但是最高的利润是以价格6卖出，这是因为1和6之间的价格差最大，如果以价格3买入则无论如何也不能获取到最高的利润。所以算法的思路可以归纳为找到一个价格的谷底，在这个谷底价格后面找到一个价格封顶，使两者的差额最大。

代码：

int maxProfit(vector<int>& prices) {
    int buy = INT_MAX;
    int profit = 0;

    for(int i = 0; i< prices.size(); i++){
        buy = min(buy, prices[i]);
        profit = max(profit, prices[i] - buy);
    }
    return profit;
}

代码分析：
在for循环中，通过min函数来找到当前股价的最低值，并保存在buy变量中，这就是当前为止买入的最低价。当前的价格减去买入的价格即为当前的利润，将当前为止最大的利润通过max函数计算出来之后保存到profit变量中。遍历完整个数组后profit即为能够获得的最大利润。因为只遍历了一遍，所以时间复杂度为O(N)。

LeetCode122 股票买卖时机问题2

题目链接：
https://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii

题目描述：
给定一个数组代表每天的股价，在可以买卖任意次数的情况下找出可以得到的最高利润(不能同时进行多项交易，即买股票前必须先卖掉所有的股票）。

例子

Input: [7,1,5,3,6,4]
Output: 7
Explanation: 在第二天以价格1买入后第三天以价格5卖出，得到利润4，然后在第四天也价格3买入第五条以价格6卖出，得到利润3，总共即为7.

题目分析：
因为可以买卖任意多次，所以只要明天的价格比今天高，就今天买入，明天卖出。即使今天卖出了还是可以买入的。这样就不会放过任何股价的上涨从而获取到最高的利润。

代码：

int maxProfit(vector<int>& prices) {
    int profit = 0;
    for(int i = 1; i < prices.size(); i++){
        if(prices[i] > prices[i - 1]){
            profit += prices[i] - prices[i - 1];
        }
    }
    return profit;
}

代码分析：
从第二天开始遍历整个数组，只要涨价了就进行今天买入明天卖出的操作就可以获取到最大的利润。因为只遍历了一遍，所以时间复杂度为O(N)。

LeetCode123 股票买卖时机问题3

题目链接：
https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iii/

题目描述：
给定一个数组代表每天的股价，在最多可以进行两次买卖的情况下找出可以得到的最高利润(不能同时进行多项交易，即买股票前必须先卖掉所有的股票）。
例子

Input: [3,3,5,0,0,3,1,4]
Output: 6
Explanation: 第四天以价格0买入第六条以价格3卖出，得到利润3；第七天以价格1买入第八天以价格4卖出得到利润3，总共为6。

题目分析：
这是一道困难级别的题目。在一次的买卖当中想要获取到最大的利润就需要在最低的价格买入最高的价格卖出，即买卖的价格差最大；第二次买卖则是在第一次卖出之后再次找到一个最大的价格差。可以假设初始拥有的资金为0，可以借钱买入股票，则在买入价格为n的股票后，手上剩余的钱即为-n， -n越大则代表买入的价格越低；而以价格m卖出之后手上剩余的钱即为m - n， m - n 越大代表获得的利润越高。只要我们在进行两次买卖操做的过程中保证两次买入和两次卖出后剩余的钱一直是最多的，那第二次卖出后手上的钱就是最大的利润。

代码：

int maxProfit(vector<int>& prices) {
    int buy1 = INT_MIN, sell1 = 0, buy2 = INT_MIN, sell2 = 0;
    for(int i=0; i < prices.size(); i++) {                     
        buy1 = max(buy1, -prices[i]);
        sell1 = max(sell1, prices[i] + buy1);        buy2 = max(buy2, sell1 - prices[i]);

        sell2 = max(sell2, prices[i] + buy2);    }

    return sell2;}

代码分析：
代码里用buy1和sell1代表第一次买卖后手上能够剩余的最多的钱，buy2和sell2代表第二次买卖后手上能够剩余的最多的钱。通过max函数保证了buy1是以最低的价格进行第一次买入，而sell1的计算方式则是为了保证在buy1买入后能获取的最大利润；因为buy2操作是在sell1之后进行的操作，所以要在使用sell1 - prices[i]来计算第二次买入后手上剩余的钱，同样通过max函数保证了buy2是以sell1之后的最低价格买入。如果对整个的过程还不是很理解，可以结合下面的表格来讲算法在心里面给跑一下，可以有更深刻的理解。由于只遍历了一遍，所以时间复杂度为O(N)。

	3	3	5	0	0	3	1	4
buy1	-3	-3	-3	0	0	0	0	0
sell1	0	0	2	2	2	3	3	4
buy2	-3	-3	-3	2	2	2	2	2
sell2	0	0	2	2	2	5	5	6

LeetCode188 股票买卖时机问题4

题目链接：
https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv/

题目描述：
给定一个数组代表每天的股价，在最多可以进行k次买卖的情况下找出可以得到的最高利润(不能同时进行多项交易，即买股票前必须先卖掉所有的股票）。
例子

Input: [3,2,6,5,0,3], k = 2
Output: 7
Explanation: 以价格2买入价格6卖出，得到利润4；以价格0买入价格3卖出，得到利润3，总共为7。

题目分析：
这同样是一道困难级别的题目。当k = 2 时，这道题目其实和上一道题是一样的。但是现在的k是不确定的，那我们能不能以相同的思路来解决这题呢? 答案当然是肯定的。我们只要创建两个大小为k + 1的数组分别用来保存每次买卖后手上剩余的最多钱即可。

代码：

int maxProfit(int k, vector<int>& prices) {
    k = min(k, (int)prices.size() / 2);
    if(k == 0) return 0;
    
    vector<int>buy(k + 1, INT_MIN);
	vector<int>sell(k + 1, 0);
	for(int i = 0; i < prices.size(); i++) {
	    for(int j = 1; j <= k; j++) {
	        buy[j] = max(buy[j], sell[j - 1] - prices[i]);
	        sell[j] = max(sell[j], buy[j] + prices[i]);
	    }
	}
	    
	return sell[k];	    
}

代码分析：
由于k的值是不确定的，所以需要对 k == 0 这种 corner case 进行处理，否则程序会报错。一次完整的交易需要买和卖两天来完成，所以最多只能进行 prices.size() / 2 次交易。这里创建了两个长度为 k + 1 的数组 buy 和sell 分别用来保存每次买卖操作后手上剩余的钱，当完成所有的遍历后最后一次卖出时剩余的钱就是最大的利润。时间复杂度也不难看出是O(k * N)。上述代码提交后总的运行时间会是600ms+, 并不是很理想还需要进一步的优化。

当k大于数组长度的一半时，这道题就转换成了股票买卖时机问题2，相当于可以买卖任意次数，这时就可以直接套用问题2的算法来减少运行时间。优化后的代码如下。

优化代码：

int maxProfit(int k, vector<int>& prices) {
    if(k > prices.size() / 2) {
        int profit = 0;
        for(int i = 1; i< prices.size(); i++){
            if(prices[i] > prices[i - 1]){
                profit += prices[i] - prices[i - 1];
            }
        }
        return profit;
    } else if(k <= 0) return 0;
    
   vector<int>buy(k + 1, INT_MIN);
	vector<int>sell(k + 1, 0);
	for(int i = 0; i < prices.size(); i++) {
	    for(int j = 1; j <= k; j++) {
	        buy[j] = max(buy[j], sell[j - 1] - prices[i]);
	        sell[j] = max(sell[j], buy[j] + prices[i]);
	    }
	}
	    
	return sell[k];	
}

优化代码分析：
上述代码将k > prices.size() / 2的情况套用过来问题2的算法，只要涨价就进行买入卖出操作，可以保证获取到所有的涨价利润，其它情况下才采用原始代码里的算法。优化后代码的运行时间为4ms, 可见优化的效果非常明显。

LeetCode309 股票买卖时机问题5

题目链接：
https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/

题目描述：
给定一个数组代表每天的股价，可以进行任意次买卖但是每次卖出后要有一天的冷却期不能买入股票。找出可以得到的最高利润(不能同时进行多项交易，即买股票前必须先卖掉所有的股票）。

题目分析：
卖出股票后有一天的冷却期，所以股票的持有状态会有三种，分别是买入、卖出和冷却。可以使用三个数组buy, sell 和 cooldown 来存储每天这三种状态下的最高利润，如sell[i]代表第 i 天卖出状态下能得到的最高利润。买入的状态可以持续多天，如第一天买入，第二天和第三天并没有卖出则这两天都是买入状态。卖出后状态转换为卖出状态，然后第二天转为冷却状态，冷却状态同样可以持续多天。

对任意一天来讲，其买入状态有两个入口：一个就是昨天买入状态的持续；另一个就是昨天冷却，今天买入，即用昨天冷却的钱减去今天的股价。具体选择哪个入口取决于哪个入口可以让今天的买入状态下保持钱最多。同样卖出状态也有两个入口：一个就是昨天的卖出状态持续；另一个就是在昨天买入状态的基础上今天卖出，即用昨天买入的钱加入今天的股价。具体选择哪个入口同样取决于哪个入口可以让今天的卖出状态下保持钱最多。冷却状态由于不做任何操作所以当天冷却状态的钱同昨天卖出状态的钱是保持一致的。用代码将上述的状态转换写出来如下：

buy[i] = max(buy[i - 1], cooldown[i - 1] - prices[i];
sell[i] = max(sell[i - 1], buy[i - 1] + prices[i];
cooldown[i] = sell[i - 1];

注意到冷却状态和卖出状态之间的关系，那 cooldown[i - 1] 就等于 sell[i - 2], 将其替换到第一行中之后就可以去掉冷却状态，将代码转换成两个状态的转换：

buy[i] = max(buy[i - 1], sell[i - 2] - prices[i];
sell[i] = max(sell[i - 1], buy[i - 1] + prices[i];

明确了买入和卖出的状态转换后就不难写出代码。

代码：

int maxProfit(vector<int>& prices) {
    int n = prices.size();
    if(n <= 0) return 0;
    vector<int>buy(n + 1, INT_MIN);
    vector<int>sell(n + 1, 0);
    buy[1] = -prices[0];
    for(int i = 2; i <= n; i++) {
        int price = prices[i - 1];
        buy[i] = max(buy[i - 1], sell[i - 2] - price);
        sell[i] = max(sell[i - 1], buy[i - 1] + price);
    }
    return sell[n];
}

代码分析：
因为代码里涉及到 -2 的下标操作，所以为了简化代码这里创建的buy和sell数组的大小都为 n + 1，并且直接将第一天buy[1] 初始化为买入的价格即 -prices[0]。然后从第二天开始遍历股价数组，同时根据上面推导出来的公式分别计算买入和卖出的最高利润。最后一次卖出就是可以获得的最高利润。由于只遍历了一遍，所以时间复杂度为O(N)。

LeetCode714 股票买卖时机问题6

题目链接：
https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/

题目描述：
给定一个数组代表每天的股价，可以进行任意次买卖但是每次买卖都需要有交易费。找出可以得到的最高利润(不能同时进行多项交易，即买股票前必须先卖掉所有的股票）。

题目分析：
这道题目同上一题非常类似，计算买入状态利润的算法是一样的，不同的就是在计算卖出状态利润时对每一次卖出操作要减去交易费。

代码：

int maxProfit(vector<int>& prices, int fee) {
    int n = prices.size();
    if(n <= 1) return 0;
    vector<int>buy(n, INT_MIN);
    vector<int>sell(n, 0);
    buy[0] = -prices[0];
    for(int i = 1; i< n; i++) {
        buy[i] = max(buy[i - 1], sell[i - 1] - prices[i]);
        sell[i] = max(sell[i - 1], buy[i - 1] + prices[i] - fee);
    }
    
    return sell[n - 1];
}

代码分析：
在上述代码中，同样创建了两个数组buy和selL来保存每天每种状态的最高利润。时间复杂度同样为O(N)，没有优化的空间，但是在空间上可以继续优化。观察状态转换部分的代码，我们完全可以使用几个变量来代替数组。优化后的代码如下所示。

优化代码：

int maxProfit(vector<int>& prices, int fee) {
    int n = prices.size();
    if(n <= 1) return 0;
    int buy(-prices[0]), sell(0), preBuy;
    for(int i = 1; i< n; i++) {
        preBuy = buy;
        buy = max(buy, sell - prices[i]);
        sell = max(sell, preBuy + prices[i] - fee);
    }
    
    return sell;
}

至此，LeetCode上的股票买卖问题就整理完了。总结起来就是需要注意股票的买和卖这两个状态，找出这两个状态的转换方式，代码就不难写出来了。