BFS计算出面积最大的矩形

发表于   |   分类于   |     |   阅读次数

很多大厂面试时都会考算法，然后招人进去了可能就干一些 ctrl+c/ctrl+v 的简单工作，所以就有了面试造飞机，实际工作拧螺丝钉的调侃说法。其实不然，虽然程序员大部分的工作可能不会涉及到算法，但是一旦遇到那些需要算法的复杂情况，如果对这个算法不熟的话可能会卡住你好几天的时间；但是如果你会这个算法的话那可能仅仅需要几个小时。前一段时间工作中就遇到了这样的一个问题最后使用了BFS算法才完美地解决了这个问题。

问题描述

当开发导航SDK的时候，需要在展示地图的同时在地图上覆盖一些View来展示一些重要的信息，如往左转，前方有收费站、服务区等。但是我们不希望这些View将地图上正在展示的一些重要的POI给遮住，这就需要我们根据这些View的大小、位置和数目来动态地调整地图的大小和中心位置，确保这些重要的POI一直处于正常的展示状态。

问题分析

问题的最终目的是在当前屏幕的范围上刨除掉所有遮挡View后，找出那个最大的矩形区域，然后调用地图的API来调整地图即可。地图API不在本文的讨论范围，所以我们仅仅关注如何找出这个矩形。
如下图所示，屏幕最初始就是一个矩形，我们以红色矩形作为遮挡View,当添加一个红色的矩形在其上面之后，最大面积的矩形就是黄色虚线框和绿色虚线框中某一个(严格意义上来讲在红色矩形的左边和上边也会有两个狭窄的矩形，但是实际中红色矩形框都是靠着四边的，最后的结果不可能在这两个狭窄的矩形中产生，所以在这里直接将其忽略掉以提高性能)，所以。根据红色矩形右下角的坐标，我们就可以计算出这两个新矩形的位置和面积。

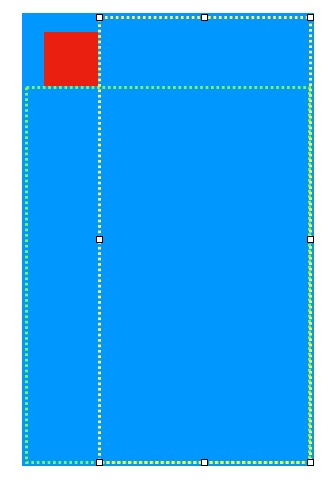
但是遮挡View可能不止一个,如果再添加一个红色矩形后，原本的黄色虚线矩形就可以被裁剪成下图中的两个黄色虚线矩形框。

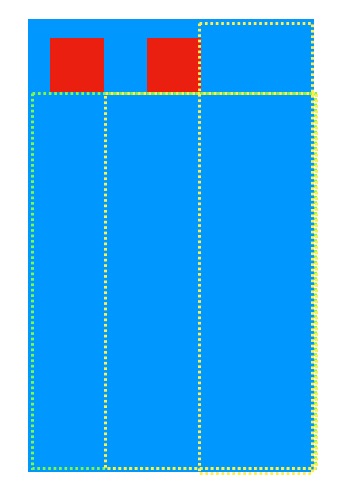
继续添加一个红色矩形后原本的绿色虚线框矩形也可以被裁剪成下图中的两个绿色虚线矩形框。

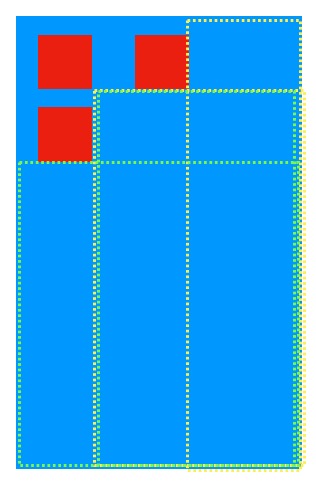
有发现规律吗？原始的一个矩形在添加一个红色矩形后，被裁剪成了两个矩形，当有新的红色矩形被添加到这两个矩形后，每个矩形又被裁剪成了两个新的矩形，这像不像二叉树呢？原始的矩形是根节点，下面会生成一些子节点，而我们就是要从所有的子节点中找到面积最大的那个，由于子节点会在遍历的过程中生成，所以我们可以使用BFS算法一层层的进行遍历。但是这并不是严格的二叉树，当红色矩形添加到矩形的中间位置的时候，其生成的子节点可能会有三个或者四个。另外就是当新添加的红色矩形和现有的矩形并没有重叠的地方时，那这个红色矩形就可以完全忽略掉，当前的节点直接复制自己生成一个新的字节点。同时这就引入了下面一个问题：如何判断两个矩形是否有互相重叠的地方？

判断两个矩形是否有互相重叠的地方

如果要直接判断两个矩形是否有互相重叠的地方会比较复杂，因为重叠的方式会有很多中，如分别有一个角重叠、两个角重叠、一个矩形包含另外一个等等，非常容易把人搞得头大。这时就可以采用反向思维的方式，什么情况下两个矩形不会有重叠的地方呢？我们以一个矩形作为基准，当它的上边线比另外一个矩形的下边线低的时候，那它们两个肯定就不会重叠；或者当它的左边线比另外一个矩形的右边线靠右的时候，那他们同样也不会重叠；同样的道理也适用于右边线和底边线。

至此，问题已经分析得很清楚了，我们只需要以原始的矩形为根节点，然后BFS遍历遮挡矩形树，每个遮挡矩形如果和当前树中的一层矩形有重叠的话就为其生成新的子接点，如果没有重叠的部分，则当前节点就复制自己作为子节点。当前一层所有矩形都遍历完成后我们就取出下一个遮挡矩形进行下一层的遍历。这棵树的深度就是遮挡矩形的数目，当遍历到最后一层的时候那个面积最大的矩形就是我们要找的目标。

算法实现

为了方便算法的实现，我们首先定义个矩形类，上下左右四个点作为其属性。按照前面的分析，我们定义了isOverLap方法来判断当前的矩形是否和其它的矩形有重叠的地方；另外还定义了几个update方法用来快速生成其子节点; 最后我们还实现了Comparable接口方便我们最后找到面积最大的矩形。代码以Kotlin实现，此外坐标系以左上角为原点，x轴向右，y轴向下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class MapOverLayRect(
  var left: Int,
  var top: Int,
  var right: Int,
  var bottom: Int
) : Comparable<MapOverLayRect> {
  fun isOverLap(reactAnother: MapOverLayRect): Boolean {
    return !(
      right <= reactAnother.left ||
        bottom <= reactAnother.top ||
        left >= reactAnother.right ||
        top >= reactAnother.bottom
      )
  }

  fun updateTop(newTop: Int): MapOverLayRect {
    return MapOverLayRect(left, newTop, right, bottom)
  }

  fun updateLeft(newLeft: Int): MapOverLayRect {
    return MapOverLayRect(newLeft, top, right, bottom)
  }

  fun updateRight(newRight: Int): MapOverLayRect {
    return MapOverLayRect(left, top, newRight, bottom)
  }

  fun updateBottom(newBottom: Int): MapOverLayRect {
    return MapOverLayRect(left, top, right, newBottom)
  }

  override fun compareTo(other: MapOverLayRect): Int {
    return (((right - left) * (bottom - top)) - ((other.right - other.left) * (other.bottom - other.top)))
  }
}

定义好了矩形类就可以使用BFS算法进行遍历并寻找最大的矩形了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
override fun bfs(): MapOverLayRect {
  val queue = LinkedList<MapOverLayRect>()
  // 将根节点入队
  queue.push(MapOverLayRect(0, 0, width, height))

  // mapOverlays 中保存着所有的遮挡矩形，对其进行遍历的同时使用BFS算法
  mapOverlays
    .forEach {
      // size 为当前层的节点数
      var size = queue.size
      // size 大于0则代表当前层没有遍历完毕
      while (size > 0) {
        // 有重叠的部分，则需要对当前矩形进行裁剪生成子节点
        val subMapRect = queue.pollFirst()
        if (it.isOverLap(subMapRect)) {
          if (it.top - subMapRect.top < subMapRect.bottom - it.bottom) {
            // 遮挡矩形在当前矩形的上半部分，将下半部分进行裁剪生成新的矩形子节点
            queue.offerLast(subMapRect.updateTop(it.bottom))
          } else if (it.top - subMapRect.top > subMapRect.bottom - it.bottom) {
            // 遮挡矩形在当前矩形的下半部分，将上半部分进行裁剪生成新的矩形子节点
            queue.offerLast(subMapRect.updateBottom(it.top))
          } else {
            // 遮挡矩形在当前矩形的中间，将上、下两部分分别进行裁剪生成新的矩形子节点
            queue.offerLast(subMapRect.updateTop(it.bottom))
            queue.offerLast(subMapRect.updateBottom(it.top))
          }

          if (it.left - subMapRect.left < subMapRect.right - it.right) {
            // 遮挡矩形在当前矩形的左半部分，将右半部分进行裁剪生成新的矩形子节点
            queue.offerLast(subMapRect.updateLeft(it.right))
          } else if (it.left - subMapRect.left < subMapRect.right - it.right) {
            // 遮挡矩形在当前矩形的右半部分，将左半部分进行裁剪生成新的矩形子节点
            queue.offerLast(subMapRect.updateRight(it.left))
          } else {
            // 遮挡矩形在当前矩形的中间，将左、右两部分分别进行裁剪生成新的矩形子节点
            queue.offerLast(subMapRect.updateLeft(it.right))
            queue.offerLast(subMapRect.updateRight(it.left))
          }
        } else {
          // 没有重叠的部分则字节以当前节点作为子节点
          queue.offerLast(subMapRect)
        }
        size--
      }
    }

// 选择最大的矩形返回
  return queue.maxOrNull()
}

总结

这就是我运用BFS算法解决工作中遇到的实际问题时的解决方案，将思路分析清楚后算法的实现并不复杂，但是如果之前没有掌握BFS算法的话可能想破脑袋也解决不了这个问题。所以大家还是要熟练掌握这些基本的算法，一方面面试的时候可以轻松应对，另一方面当工作中真的遇到需要算法解决的问题时也不至于浪费太多的脑力和时间还解决不了结果导致辛辛苦苦加班哦。
signature.png